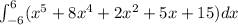Answer:
The area of the region is 25,351
 .
.
Explanation:
The Fundamental Theorem of Calculus: if
 is a continuous function on
is a continuous function on
![[a,b]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dyyh30s5r4ox0wg76shisxuulr9zptlacg.png) , then
, then
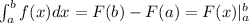
where
 is an antiderivative of
is an antiderivative of
 .
.
A function
 is an antiderivative of the function
is an antiderivative of the function
 if
if
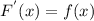
The theorem relates differential and integral calculus, and tells us how we can find the area under a curve using antidifferentiation.
To find the area of the region between the graph of the function
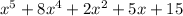 and the x-axis on the interval [-6, 6] you must:
and the x-axis on the interval [-6, 6] you must:
Apply the Fundamental Theorem of Calculus