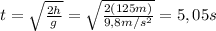Question

Um corpo de massa m= 2,0Kg é lançado horizontalmente, de uma altura h= 125m, com velocidade de módulo Vo =10m/s, como mostra a figura. Desprezando a resistência do ar e adotando g= 10m/s2 , determine: a) A energia mecânica total do corpo; b) A energia cinética do corpo a meia altura em relação ao solo; c) O tempo gasto até que o corpo atinja o solo; d) O alcance do movimento.

Answer 1

A) E = 2550 J

B) K = 1325 J

C) t = 5,05 s

Step-by-step explanation:

A) The total mechanical energy is given by the sum of the gravitational potential energy and the kinetic energy of the body:

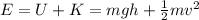`E=U+K=mgh+(1)/(2)mv^2` (1)

m: mass of the body = 2,0 kg

g: gravitational acceleration = 9,8 m/s^2

h: height = 125 m

v: initial velocity of the body = 10 m/s

You replace the values of all variables h, m, g and v in the equation (1):

`E=(2,0kg)(9,8m/s^2)(125m)+(1)/(2)(2,0kg)(10m/s)^2=2550\ J`

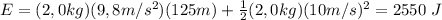
the total mechanical energy is 2550 J

B) The kinetic energy of the corp, when it is at a height of h/2 is given by:

`K=(1)/(2)mv^2`

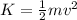
where

`v=√((v_x)^2+(v_y)^2)`

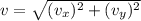
The x component of the velocity is constant in the complete trajectory, which is the initial velocity, that is, vo = vx

The y component is given by:

`v_y^2=v_(oy)^2+2gy`

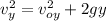
voy: vertical initial velocity = 0m/s

y: height = h/2 = 125/2 = 62.5 m

`v_y=\sqrt{2g(h)/(2)}=√(2(9.8m/s^2)(62.5m))=35m/s`

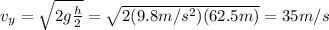
Then, you can calculate the velocity of the body and next, you can calculate the kinetic energy:

`v=√((10m/s)^2+(35m/s)^2)=36,40(m)/(s)\\\\K=(1)/(2)(2,0kg)(36,40m/s)^2=1325\ J`

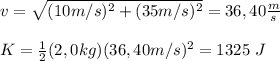
C) The time that body takes in all its trajectory is:

`t=\sqrt{(2h)/(g)}=\sqrt{(2(125m))/(9,8m/s^2)}=5,05s`