Question

What is the first step in solving the quadratic equation x2 – 40 = 0?A) taking the square root of both sides of the equationB) adding 40 to both sides of the equationC) squaring both sides of the equationD) subtracting 40 from both sides of the equation

Answer 1

The correct answer is "B", we first need to add 40 to both sides of the equation.

Explanation:

Since we have the following quadratic equation:

`x^2 - 40 = 0`

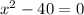
The first step to solve it is to isolate the independent variable, "x". To do that we must add +40 on both sides of the equation, since that way the "-40" on the left will be gone in a way that maintains the validity of the equation as shown below:

`x^2 - 40 = 0\\x^2 - 40 + 40 = 40\\x^2 = 40`

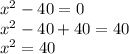
After this step we take the square root of both sides:

`√(x^2) = √(40)\\x = \pm √(40)\\x = \pm √(4*10)\\x = \pm 2*√(10)`

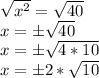
Therefore the correct answer is "B".