Question

3. The wildlife department has been feeding a special food to rainbow trout finger lings in a pond. A sample of the weight of 40 trout revealed that the mean weight is 402.7 grams and the standard deviation 8.8 grams. ( 4 POINTS) 1. What is the point estimated mean weight of the population? What is that estimate called? 2. What is the 99 percent confidence interval? 3. What are the 99 percent confidence limits? 4. Interpret your findings?

Answer 1

1) 402.7 grams. This estimate is called the sample mean.

2) (399.11, 406.29)

3) The 99 percent confidence limits is between 399.11 grams and 406.29 grams.

I am 99% sure that the value lies between 399.11 grams and 406.29 grams.

Step-by-step explanation:

sample size (n) = 40, the mean weight (x)= 402.7 grams and the standard deviation (σ)=8.8 grams

1) The point estimated mean weight of the population is 402.7 grams. This estimate is called the sample mean.

2) c = 99% = 0.99

α = 1 - 0.99 = 0.01

`(\alpha )/(2) =(0.01)/(2) =0.005`.

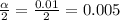The z score of 0.005 corresponds with the z score of 0.495 (0.5 - 0.005).

`z_(\alpha )/(2) =2.58`.

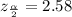The margin of error (e) =
`z_(\alpha )/(2)*(\sigma)/(√(n) ) =2.58*(8.8)/(√(40) ) =3.59`

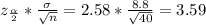
The confidence interval = x ± e = 402.7 ± 3.59 = (399.11, 406.29)

3) The 99 percent confidence limits is between 399.11 grams and 406.29 grams.

I am 99% sure that the value lies between 399.11 grams and 406.29 grams.