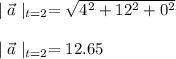Question

A girl operates a radio-controlled model car in a vacant parking lot. The girl's position is at the origin of the xy coordinate axes, and the surface of the parking lot lies in the x-y plane. The motion of the car is defined by the position vector r = (2 + 2t2)i + (6 + t3 )j where r and t are expressed in meters and seconds, respectively. Determine (a) the distance between the car and the girl when t = 2s, (b) the distance the car traveled in the interval from t = 0 to t = 2s, (c) the speed and direction of the car's velocity at t = 2s, (d) the magnitude of the car's acceleration at t = 2s.

Answer 1

a) 17.20

b) 11.31

c) 14.42

d) 12.65

Step-by-step explanation:

(a)

The girl is at the origin of the x,y coordinates (i.e 0,0,0 )

the position vector of the car at time 't' secs is

`\vec{r}= 2+2t^2, 6+t^3,0`

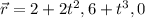
at t=2s, the position vector is

`\vec{r}= 10, 14,0`

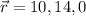
Therefore, the the distance between the car and the girl is

`s= √((10-0)^2+(14-0)^2+(0-0)^2))\`

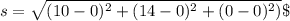
s = 17.20

(b)

The position of the car at t = 0s is
`\vec{r}_0 = 2,6,0`

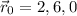
The position of the car at t = 2s is
`\vec{r}_2 = 10,14,0`

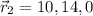
The distance of the car traveled in the interval from t=0s to t=2 s is as follows:

`s_(02)= √((10-2)^2+(14-6)^2+(0-0)^2)) \\ \\ s_(02) = 11.31`

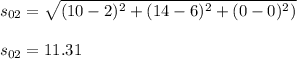
(c)

The position vector of the car at time 't' secs is

`\vec{r}= 2+2t^2, 6+t^3,0`

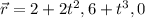
The velocity of the car is

`\vec{v}=\frac{d\vec{r}}{dt}= 4t, 3t^2,0`

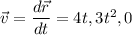
the direction of the car's velocity at t = 2s is going to be

`\vec{v}\mid _t=2 8, 12,0`

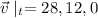
Thus; The speed of the car is

`v_(t=2)= √(8^2+12^2+0^2) \\ \\ v_(t=2)= 14.42`

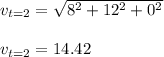
(d) the car's acceleration is:

`\vec{a}=\frac{d\vec{v}}{dt}= 4, 6t,0`

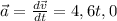
The magnitude of car's acceleration at t=2s is

`\mid \vec{a}\mid _(t=2)=√(4^2+12^2+0^2) \\ \\ \mid \vec{a}\mid _(t=2)= 12.65`