Answer:
1. 39068.07 N
2. 19534.036 N
Step-by-step explanation:
depth of water h = 10 m
atmospheric pressure Patm = 101325 Pa
density of water p = 1000 kg/m^3
acceleration due to gravity g = 9.81 m/s^2
pressure due to depth of water = pgh
P = 1000 x 9.81 x 10 = 98100 Pa
total pressure on the bottom of the tank is Patm + p = 101325 + 98100 = 199425 Pa
Left plug has diameter = 50 cm = 0.5 m
radius = 0.5/2 = 0.25 m
height = 1 cm = 0.01 m
height below tank surface = 10 - 0.01 = 9.99
pressure at this depth = 1000 x 9.81 x 9.99 = 98001.9 Pa
total pressure = Patm + P = 101325 + 98001.9 = 199326.9 Pa
surface area of plug = π
 = 3.142 x
= 3.142 x
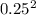 = 0.196
= 0.196

force required to lift left plug = pressure x area
F = 199326.9 x 0.196 = 39068.07 N
The right side is a hemisphere with the same diameter, therefore surface area is half of the left plug
A = 0.196/2 = 0.098

force F required to lift right plug = 199326.9 x 0.098 = 19534.036 N