answer: x =
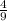
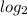 (6x) -
(6x) -
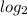 (
(
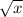 ) = 2
) = 2
expand the expression:
transform the expression:
calculate the difference:
multiply both sides by 2:
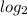 (6) +
(6) +
 *
*
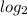 (x) = 2 is now 2
(x) = 2 is now 2
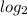 (6) +
(6) +
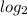 (x) = 4
(x) = 4
transform the expression:
simplify the expression:
evaluate the power:
convert the logarithm into exponential form:
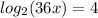 is now
is now

evaluate the power:
divide both sides by 36: