Question

11. Rocco and Biff are two koalas sitting at the

top of two eucalyptus trees, which are
located 10 m apart, as shown. Rocco's tree
is exactly half as tall as Biff's tree. From
Rocco's point of view, the angle separating
Biff and the base of his tree is 70°. How high off the ground is each koala?

Answer 1

Biff height = 9.48m

Rocco's height= 4.74m

Explanation:

As Rocco's tree is half as tall as Biff's tree, draw a horizontal line from Rocco on Rocco's tree which intersects the Biff's tree at he middle.

The angle 70 degrees is divided by 2 because of the horizontal line.

An upper right angle triangle is form by Rocco (point A), Midpoint of Biff's tree(point B), and Biff (point C).

As

`tan\theta = (perpendicular)/(base\\)`

where θ=35 and base= 10m

`tan35=(perpendical)/(10)`

`(tan35)(10)=perpendicular\\perpendicular=4.74`

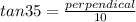
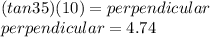
As the perpendicular found is that of a triangle formed from midpoint of Biff's, to find the total height, multiply the found perpendicular with 2.

Biff height = 4.74*2 = 9.48m

Rocco's height is half of biff height

Rocco's height= 9.48/2 = 4.74m

Answer 2

Biff's tree is 14 m off the ground and Rocco's tree is 7 m off the ground.

Explanation:

Let the height of Biff's tree be represented by x, so that the height of Rocco's tree is
`(x)/(2)`.

Draw a straight line from Rocco's point of view to a point t to the middle of Biff's tree. This line divides x into two equal parts, and the angle is divided into
`35^(0)` each.

By alternate angle property,

Tan
`35^(0)` =
`((x)/(2) )/(10)`

`(x)/(2)` = Tan
`35^(0)` × 10

= 7.00021

⇒ x = 2 × 7.0021

= 14. 0042

x = 14

Therefore, Biff's tree is 14 m off the ground and Rocco's tree is 7 m off the ground.