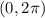Answer:
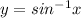
Explanation:
Given: A point is
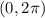
To find: function whose graph passes through the given point
Solution:
A trigonometry explains the relationship between the sides and the angles of the triangle.
The inverse trigonometric functions
 help to find the value of an unknown angle of a right triangle when length of two sides are given.
help to find the value of an unknown angle of a right triangle when length of two sides are given.
Consider

Put
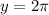

So, point
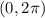 satisfies the function
satisfies the function
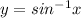
Therefore, graph of function
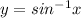 passes through
passes through