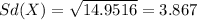Answer:
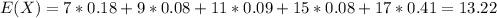
And we can find the second moment with this formula:
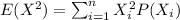
And replacing we got:
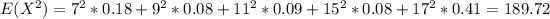
And we can find the variance like this:
![Var(X) = E(X^2) -[E(X)]^2= 189.72- (13.22)^2 =14.9516](https://img.qammunity.org/2021/formulas/mathematics/college/ku19kfajcjtcl2l8y6p4ownw5oxnzwqi1a.png)
And the deviation would be:
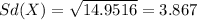
Explanation:
For this case we have the following dataset given:
Payment $7 $9 $11 $13 $15 $17
Probability 0.18 0.08 0.09 0.16 0.08 0.41
For this case we can calculate the mean with this formula:
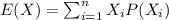
And replacing we got:
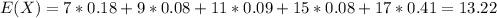
And we can find the second moment with this formula:
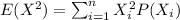
And replacing we got:
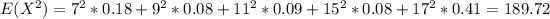
And we can find the variance like this:
![Var(X) = E(X^2) -[E(X)]^2= 189.72- (13.22)^2 =14.9516](https://img.qammunity.org/2021/formulas/mathematics/college/ku19kfajcjtcl2l8y6p4ownw5oxnzwqi1a.png)
And the deviation would be: