Answer:
a) 20
b) elastic
c) 8
d) elastic
Step-by-step explanation:
Given that q = f ( p ) =
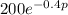
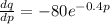
a) The elasticity of demand is given as:
Elasticity of demand =

At p =$50,
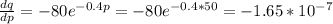
q = f ( p ) =
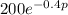 =
=
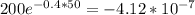
Elasticity of demand =
 =
=
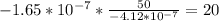
b) At p = $50, it is elastic Since Elasticity of demand is greater than 1 it is elastic. That is the price have a big effect on the quantity
c) The elasticity of demand is given as:
Elasticity of demand =

At p =$20,

q = f ( p ) =
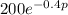 =
=
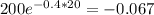
Elasticity of demand =
 =
=
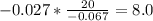
d) At p = $20, it is elastic Since Elasticity of demand is greater than 1 it is elastic