Answer:
Explanation:
Hello!
The random sample of n= 16 participants was asked to taste test two different sodas cans and rate them on a scale from 1 to 10. The cans contained the same type of soda but differ in color.
Since each participant tasted and ranked the two types of soda cans, you have per person a pair of data (X₁;X₂):
Where
X₁: Rank given to the red soda.
X₂: Rank given to the blue soda.
As said, the data is arranged in pairs per experimental unit, so these two variables are dependent, to study them is best to determine a third variable, the difference between X₁ and X₂:
Xd: X₁ - X₂
Assuming Xd~N(μd;σd²)
The objective is to test if there is any difference between the ratings based on the can color. The statistic hypotheses are:
H₀: μd=0
H₁: μd≠0
To calculate the descriptive statistics you have to calculate first the difference of each pair of ratings (see table in attachment)
Mean:
X[bar]d= ∑Xd/n= -6/16= -0.38
Variance
![S_d^2=(1)/(n-1) [sumX_d^2-((sumXd)^2)/(n) ]= (1)/(15)[64-((-6))/(^16) ]= 4.12](https://img.qammunity.org/2021/formulas/mathematics/college/enw32cfxbbs853vzwlc60qmyx0usfzbzjx.png)
Standard deviation
Sd= √4.12= 2.03
Statistic
![t= (X[bar]_d-Mu_d)/((Sd)/(√(n) ) ) ~~t_(n-1)](https://img.qammunity.org/2021/formulas/mathematics/college/vaopztlrhz6vkovy0lunflxj2089hft7sz.png)
Df: n-1= 16-10 15
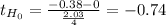
P-value:
P(t₁₅≤-0.74) + P(t₁₅≥0.74)= P(t₁₅≤-0.74) + (1 - P(t₁₅≤0.74))= 0.2354 + (1 - 0.7646)= 0.4708
The decision rule for the p-value approach is:
If p-value ≤ α, reject the null hypothesis.
If p-value > α, do not reject the null hypothesis.
α: 0.05
The p-value is greater than the level of significance, the decision is to not reject the null hypothesis.
At a 5% significance level, there is no significant evidence to reject the null hypothesis. You can conclude that there is no difference between the rankings of the red and blue cans. I.e. there is no evidence to suggest that the can color changes the average ranting of the soda.
I hope this helps!