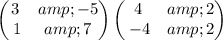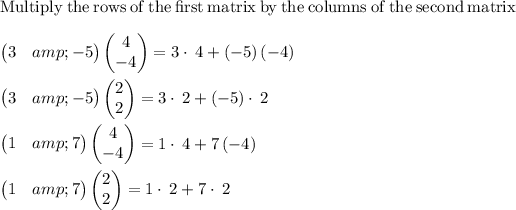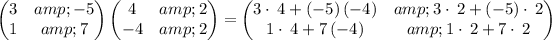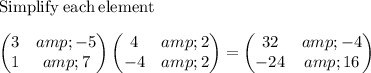Question

Find the product or type
"impossible".
3 -5 4 2
​

Answer 1

The product of
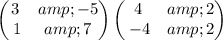`\begin{pmatrix}3&-5\\ \:1&7\end{pmatrix}\begin{pmatrix}4&2\\ \:-4&2\end{pmatrix}` is
`\begin{pmatrix}32&-4\\ -24&16\end{pmatrix}`.

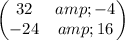Explanation:

A matrix is a rectangular arrangement of numbers into rows and columns.

Matrix multiplication refers to the product of two matrices.

The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one.

To find the product of
`\begin{pmatrix}3&-5\\ \:1&7\end{pmatrix}\begin{pmatrix}4&2\\ \:-4&2\end{pmatrix}`

`\mathrm{Multiply\:the\:rows\:of\:the\:first\:matrix\:by\:the\:columns\:of\:the\:second\:matrix}\\\\\begin{pmatrix}3&-5\end{pmatrix}\begin{pmatrix}4\\ -4\end{pmatrix}=3\cdot \:4+\left(-5\right)\left(-4\right)\\\\\begin{pmatrix}3&-5\end{pmatrix}\begin{pmatrix}2\\ 2\end{pmatrix}=3\cdot \:2+\left(-5\right)\cdot \:2\\\\\begin{pmatrix}1&7\end{pmatrix}\begin{pmatrix}4\\ -4\end{pmatrix}=1\cdot \:4+7\left(-4\right)\\\\\begin{pmatrix}1&7\end{pmatrix}\begin{pmatrix}2\\ 2\end{pmatrix}=1\cdot \:2+7\cdot \:2`

`\begin{pmatrix}3&-5\\ 1&7\end{pmatrix}\begin{pmatrix}4&2\\ -4&2\end{pmatrix}=\begin{pmatrix}3\cdot \:4+\left(-5\right)\left(-4\right)&3\cdot \:2+\left(-5\right)\cdot \:2\\ 1\cdot \:4+7\left(-4\right)&1\cdot \:2+7\cdot \:2\end{pmatrix}`

`\mathrm{Simplify\:each\:element}\\\\\begin{pmatrix}3&-5\\ 1&7\end{pmatrix}\begin{pmatrix}4&2\\ -4&2\end{pmatrix}=\begin{pmatrix}32&-4\\ -24&16\end{pmatrix}`