Question

Combustion analysis of a 13.42-g sample of an unknown organic compound (which contains only carbon, hydrogen, and oxygen) produced 36.86 g CO2 and 10.06 g H2O. The molar mass of the compound is 288.38 g/mol . Part A Find the molecular formula of the unknown compound. Express your answer as a chemical formula.

Answer 1

Molecular mass =
`C_(6) H_(8) O_(16)`

Step-by-step explanation:

`((36.86gCO_(2) )/(44g/molCO_(2) ))`
`((10.06gH_(2)O)/(18g/molH_(2)O) )`

(0.8377mol of CO2) (0.556 mol of H2O)

mole ratio of CO2 to H2O = 1.5 : 1 ≅ 3 : 2

`(CO_(2) )_(3) , (H_(2) O)_(2)`

⇒
`(C_(3) H_(4) O_(8) )_(x)` = 288.38

(12 × 3 + 1 × 4 + 16 × 8)x = 288.38

168x = 288.38

x = 1.71 ≅ 2

∴ Molecular mass =
`C_(6) H_(8) O_(16)`

Answer 2

`C_(18)H_(24)O_3`

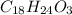
Step-by-step explanation:

Hello,

In this case, combustion analyses help us to determine the empirical formula of a compound via the quantification of the released carbon dioxide and water since the law of conservation of mass is leveraged to attain it. In such a way, as 36.86 g of carbon dioxide were obtained, this directly represents the mass of carbon present in the sample, thus, we first compute the moles of carbon:

`n_(C)=36.86gCO_2*(1molCO_2)/(44gCO_2) *(1molC)/(1molCO_2) =0.838molC`

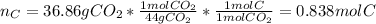
Then, into the water one could find the moles of hydrogen:

`n_(H_2O)=10.06gH_2O*(1molH_2O)/(18gH_2O)*(2molH)/(1molH_2O) =1.12molH`

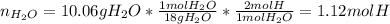
Now, we compute the moles of oxygen by firstly computing the mass of oxygen:

`m_(O)=13.42g-36.86gCO_2*(12gC)/(44gCO_2) -10.06 gH_2O*(2gH)/(18gH_2O) =2.25gO`

`n_O=2.25gO*(1molO)/(16gO) =0.141molO`

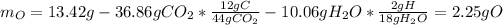
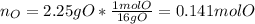
Then, we have the mole ratio:

`C_(0.838)H_(1.12)O_(0.141)\rightarrow C_6H_8O`

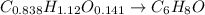
Whose molar mass is 12x6+1x8+16=96 g/mol, but the whole compound molar mass is 288.38, the factor is 288.38/96 =3, Therefore the formula:

`C_(18)H_(24)O_3`

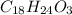
Regards.