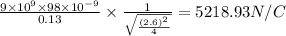Answer:
By exact formula
5076.59N/C
And by approximation formula
5218.93N/C
Step-by-step explanation:
We are given that
Length of rod,L=2.6 m
Charge,q=98nC=
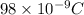
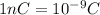
a=13 cm=0.13 m
1 m=100 cm
By exact formula
The magnitude of the electric field due to the rod at a location 13 cm from the midpoint of the rod=
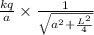
Where k=

Using the formula
The magnitude of the electric field due to the rod at a location 13 cm from the midpoint of the rod=
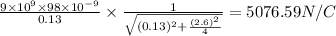
In approximation formula
a<<L
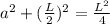
Therefore,the magnitude of the electric field due to the rod at a location 13 cm from the midpoint of the rod=

The magnitude of the electric field due to the rod at a location 13 cm from the midpoint of the rod=