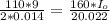Question

Two circular coils are concentric and lie in the same plane. The inner coil contains 110 turns of wire, has a radius of 0.014 m, and carries a current of 9.0 A. The outer coil contains 160 turns and has a radius of 0.022 m. What must be the magnitude of the current in the outer coil, such that the net magnetic field at the common center of the two coils is zero?

Answer 1

The current flowing through the outer coils is

Step-by-step explanation:

From the question we are told that

The number of turn of inner coil is
`N _i = 110 \ turns`

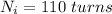
The radius of inner coil is
`r_i = 0.014 \ m`

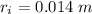
The current flowing through the inner coil is
`I_i = 9.0 \ A`

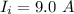
The number of turn of outer coil is
`N_o = 160 \ turns`

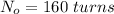
The radius of outer coil is
`r_o = 0.022\ m`

For net magnetic field at the common center of the two coils to be zero the current flowing in the outer coil must be opposite to current flowing inner coil

The magnetic field due to inner coils is mathematically represented as

`B_i = (N_i \mu I)/(2 r_i)`

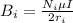
The magnetic field due to inner coils is mathematically represented as

`B_o = (N_o \mu I_o)/(2 r_o)`

Now for magnetic field at center to be zero

`B_o = B_i`

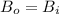
So

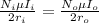
`(N_i \mu I_i)/(2 r_i) = (N_o \mu I_o)/(2 r_o)`

=>
`(110 * 9)/(2 * 0.014) = (160 *I_o)/(2 0.022)`

`I_o = 9.72 \ A`