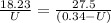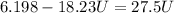Question

Two long, parallel, current-carrying wires lie in an xy-plane. The first wire lies on the line y = 0.340 m and carries a current of 27.5 A in the +x direction. The second wire lies along the x-axis. The wires exert attractive forces on each other, and the force per unit length on each wire is 295 µN/m. What is the y-value (in m) of the line in the xy-plane where the total magnetic field is zero?

Answer 1

The y-value of the line in the xy-plane where the total magnetic field is zero
`U = 0.1355 \ m`

Step-by-step explanation:

From the question we are told that

The distance of wire one from two along the y-axis is y = 0.340 m

The current on the first wire is
`I_1 = (27.5i) A`

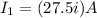
The force per unit length on each wire is
`Z = 295 \mu N/m = 295*10^(-6) N/m`

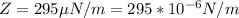
Generally the force per unit length is mathematically represented as

`Z = (F)/(l) = (\mu_o I_1I_2)/(2\pi y)`

=>
`(\mu_o I_1I_2)/(2\pi y) = 295`

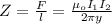
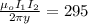
Where
`\mu_o` is the permeability of free space with a constant value of
`\mu_o = 4\pi *10^(-7) \ N/A2`

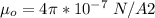
substituting values

`( 4\pi *10^(-7) 27.5 * I_2)/(2\pi * 0.340) = 295 *10^(-6)`

=>
`I_2 = 18.23 \ A`

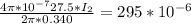
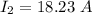
Let U denote the line in the xy-plane where the total magnetic field is zero

So

So the force per unit length of wire 2 from line U is equal to the force per unit length of wire 1 from line (y - U)

So

`(\mu_o I_2 )/(2 \pi U) = (\mu_o I_1 )/(2 \pi(y - U) )`

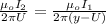
substituting values

`( 18.23 )/( U) = ( 27.5 )/((0.34 - U) )`

`6.198 -18.23U = 27.5U`

`6.198=45.73U`

`U = 0.1355 \ m`