Question

Two loudspeakers are located 2.65 m apart on an outdoor stage. A listener is 19.1 m from one and 20.1 m from the other. During the sound check, a signal generator drives the two speakers in phase with the same amplitude and frequency. The transmitted frequency is swept through the audible range (20 Hz–20 kHz). The speed of sound in the air is 343 m/s. What are the three lowest frequencies that give minimum signal (destructive interference) at the listener's location?

Answer 1

171.5Hz,514.5Hz and 857.5Hz

Step-by-step explanation:

We are given that

Distance between two loudspeaker,d=2.65 m

Distance of listener from one end=19.1 m

Distance of listener from other end=20.1 m

`\Delta L=20.1-19.1=1`m

Speed of sound,v=343m/s

For destructive interference

`f_(min,n)=((n-0.5)v)/(\Delta L)`

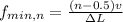
Using the formula and substitute n=1

`f_(min,1)=((1-0.5)* 343)/(1)=171.5Hz`

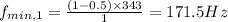
For n=2

`f_(min,2)=((2-0.5)* 343)/(1)=514.5Hz`

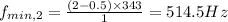
For n=3

`f_(min,3)=(3-0.5)* 343=857.5Hz`

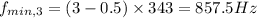
Hence, the three lowest frequencies that give minimum signal (destructive interference) at the listener's location is given by

171.5Hz,514.5Hz and 857.5Hz