Question

Let’s consider tunneling of an electron outside of a potential well. The formula for the transmission coefficient is T \simeq e^{-2CL}T≃e ​−2CL ​​ , where L is the width of the barrier and C is a term that includes the particle energy and barrier height. If the tunneling coefficient is found to be T = 0.050T=0.050 for a given value of LL, for what new value of L\text{'}L’ is the tunneling coefficient T\text{'} = 0.025T’=0.025 ? (All other parameters remain unchanged.) Express L\text{'}L’ in terms of the original LL.

Answer 1

L' = 1.231L

Step-by-step explanation:

The transmission coefficient, in a tunneling process in which an electron is involved, can be approximated to the following expression:

`T \approx e^(-2CL)`

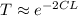
L: width of the barrier

C: constant that includes particle energy and barrier height

You have that the transmission coefficient for a specific value of L is T = 0.050. Furthermore, you have that for a new value of the width of the barrier, let's say, L', the value of the transmission coefficient is T'=0.025.

To find the new value of the L' you can write down both situation for T and T', as in the following:

`0.050=e^(-2CL)\ \ \ \ (1)\\\\0.025=e^(-2CL')\ \ \ \ (2)`

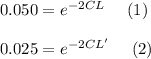
Next, by properties of logarithms, you can apply Ln to both equations (1) and (2):

`ln(0.050)=ln(e^(-2CL))=-2CL\ \ \ \ (3)\\\\ln(0.025)=ln(e^(-2CL'))=-2CL'\ \ \ \ (4)`

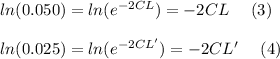
Next, you divide the equation (3) into (4), and finally, you solve for L':

`(ln(0.050))/(ln(0.025))=(-2CL)/(-2CL')=(L)/(L')\\\\0.812=(L)/(L')\\\\L'=(L)/(0.812)=1.231L`

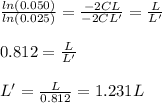
hence, when the trnasmission coeeficient has changes to a values of 0.025, the new width of the barrier L' is 1.231 L