Question

A certain federal agency employs three consulting firms (A, B and C) with probabilities 0.40, 0.45 and 0.15. From past experiences, it is known that the probability of cost overruns for the firms are 0.01, 0.14, and 0.17, respectively. Suppose that a cost overrun is experienced by the agency. What is the probability that the firm involved is firm B

Answer 1

68.11% probability that the firm involved is firm B

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

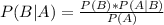
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Cost overrun

Event B: Agency B used.

A certain federal agency employs three consulting firms (A, B and C) with probabilities 0.40, 0.45 and 0.15.

This means that
`P(B) = 0.45`

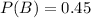
From past experiences, it is known that the probability of cost overruns for the firms are 0.01, 0.14, and 0.17, respectively.

This means that
`P(A|B) = 0.14`

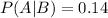
Probability of cost overrun.

Firm A is used 40% of the time, with 1% of these having cost overrun. B is used 45%, with 14% of these having cost overruns. C is used 15% of the time, with 17% of these having cost overruns.

So

`P(A) = 0.4*0.01 + 0.45*0.14 + 0.15*0.17 = 0.0925`

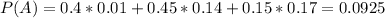
What is the probability that the firm involved is firm B

`P(B|A) = (0.45*0.14)/(0.0925) = 0.6811`

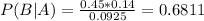
68.11% probability that the firm involved is firm B