Answer:
t = 4 s
Explanation:
Given function:
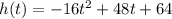
where:
- h = height of the ball (in feet)
- t = time (in seconds)
When the ball hits the ground, its height will be 0 ft.
Therefore, set the function to zero and solve for t:
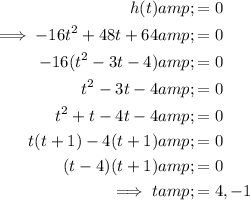
As time is positive, t = 4 s (only).