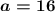Question

Using the distributive property to find the product (y−4x)(y2+4y+16) results in a polynomial of the form y3+4y2+ay−4xy2−axy−64x. What is the value of a in the polynomial?

Answer 1

16

Step-by-step explanation:

Answer 2

Answer: a = 16

==========================================================

Step-by-step explanation:

Let's expand out that given expression.

First I'll let w = y-4x to make distribution a bit easier

`(y-4x)(y^2+4y+16)\\\\w(y^2+4y+16)\\\\wy^2+4wy+16w\\\\`

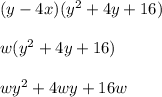
Now plug w = y-4x back in and distribute three more times

`wy^2+4wy+16w\\\\y^2(w)+4y(w)+16(w)\\\\y^2(y-4x)+4y(y-4x)+16(y-4x)\\\\y^3-4xy^2+4y^2-\boldsymbol{16}xy+16y-64x\\\\`

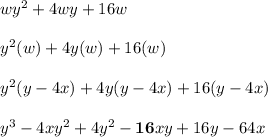
Notice that the only
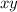`xy` term here is the
`-16xy`

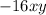
Comparing this to the form
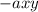`-axy` shows that
`\boldsymbol{a = 16}`