Question

4. Automobile policies are separated into two groups: low-risk and high-risk. Actuary Rahul examines low-risk policies, continuing until a policy with a claim is found and then stopping. Actuary Toby follows the same procedure with high-risk policies. Each low-risk policy has a 10% probability of having a claim. Each high-risk policy has a 20% probability of having a claim. The claim statuses of polices are mutually independent. Calculate the probability that Actuary Rahul examines fewer policies than Actuary Toby.

Answer 1

Explanation:

for n ∈ N

Since Actuary Rahul examines low-risk policies, continuing until a policy with a claim is found and then stopping.

∴ the probability that Actuary Rahul examines exactly n policies

`(0.9)^(n-1).(0.1)---(1)`

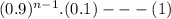
the probability that Actuary Toby examines more than exactly n policies

`(0.8)^n---(2)`

Given that policies are actually independent

∴ the probability that the event (1) and (2) happens simultaneously is

`(0.9)^(n-1)*(0.1)*(0.8)^n`

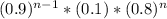
∴ the probability that Actuary Rahul examines fewer policies than Actuary Toby

`\sum ^\infty _(n=1) (0.9)^(n-1)*(0.1)*(0.8)^n\\\\=((0.1)/(0.9) \sum ^\infty _(n=1)(0.72)^n\\\\=(1)/(9) ((0.72)/(0.28) )\\\\=(2)/(7) \\\\=0.2857`

the probability that Actuary Rahul examines fewer policies than Actuary Toby is 0.2857