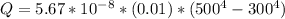Answer:
The heat rate is
Step-by-step explanation:
From the question we are told that
The surface emissivity is

The length is
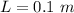
The width is
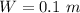
The surface temperature of one side is

The temperature of the quiescent air

The temperature of the surrounding is
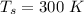
The heat rate from the flat plate is mathematically represented as
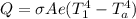
Where
 is the quiescent air Stefan-Boltzmann constant and it value is
is the quiescent air Stefan-Boltzmann constant and it value is
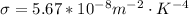
A is the area which is mathematically evaluated as
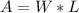
substituting values
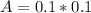
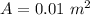
substituting values