Question

Giraffes have excellent vision. Refer to the African Zoology (Oct. 2013) study of a giraffe’s eyesight. Recall that the researchers measured the eye mass for a sample of 27 giraffes native to Zimbabwe, Africa, and found x = 53.4 grams and s = 8.6 grams. Suppose the objective is to sample enough giraffes in order to obtain an estimate of the mean eye mass to within 3 grams of its true value with a 99% confidence interval.A. Identify the cofidence coefficient for this study. B. Identify the desired sampling error for this study. C. Fnd the sample size required to obtain the desired estimate of the true mean.

Answer 1

(a) The confidence coefficient is 2.779.

(b) The desired sampling error for this study is the margin of error, ±3.

(c) The sample size required to obtain the desired estimate of the true mean is 55.

Explanation:

The information provided is:

`\bar x=53.4\ \text{grams}\\s=8.6\ \text{grams}\\n=27\\\text{Confidence Level} = 99\%`

(a)

As the sample size is n = 27 < 30 and the population standard deviation is not provided a t-interval would be used to estimate the true mean.

So, the confidence coefficient for the 99% confidence interval for true mean is:

`t_(\alpha/2, (n-1))=t_(0.01/2, (27-1))=t_(0.005, 26)=2.779`

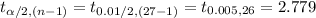
*Use the t-table.

Thus, the confidence coefficient is 2.779.

(b)

The error caused due to incorrect sample selection, i.e. a sample that is not a true representative of the population is known as the sampling error.

In this case the sampling error is known as the margin of error of the confidence interval.

The margin of error is:

MOE = 3 grams

Thus, the desired sampling error for this study is the margin of error, ±3.

(c)

Assume that the ample size required to obtain the desired estimate of the true mean is quite large, such that the sampling distribution of sample mean follows a normal distribution according to the central limit theorem.

Then the margin of error for a z-interval for mean is:

`\text{MOE}=z_(\alpha/2)* (s)/(√(n))`

MOE = 3 grams

The critical value of z for 99% confidence level is:

`z_(\alpha/2)=z_(0.01/2)=z_(0.005)=2.58`

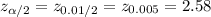
*Use a z-table.

Compute the sample size as follows:

`\text{MOE}=z_(\alpha/2)* (s)/(√(n))`

`n=[(z_(\alpha/2)* s)/(MOE)]^(2)`

`=[(2.58* 8.6)/(3)]^(2)\\\\=54.700816\\\\\approx 55`

Thus, the sample size required to obtain the desired estimate of the true mean is 55.