Question

A man 2 m high observes the angle of elevation to the top of a building to be 71° and the angle of depression to the bottom of the building to be 26°. How tall is the building?

Answer 1

The building is 13.91 m tall

Explanation:

The parameters given are;

Angle of elevation to the top of the building = 71°

Angle of depression to the bottom of the building = 26°

Height of the man = 2 m

Therefore, the sight of the man, the man's height, and the distance of the man from the building forms a triangle where:

The hypotenuse side = The sight of the man to the bottom of the building

Hence;

In ΔABC, A being at the eye level or head level of the man, B at the foot and C at the bottom of the building

∴ ∠A + Angle of depression to the bottom of the building = 90°

∠A = 90° - 26° = 64°

∠B = 90° and ∠C = 26° (Sum of angles in a triangle)

`Tan(C) = (AB)/(BC)`

Distance of the man from the building = BC

`Tan(26) = (2)/(BC)`

`BC= (2)/( Tan(26) ) = 4.1 \, m`

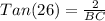
Given that the angle of elevation to the top of the building = 71°, we have;

ΔAET

Where:

A is at the head level of the man,

E is the point on the building directing facing the man and

T is the top of the building

Hence AE = BC and ∡TAE = 71°

TE + AB= The height of the building

`Tan(TAE) = (TE)/(AE)\\\\Tan(71) = (TE)/(4.1)`

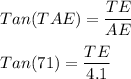
∴ TE = tan(71°) × 4.1 = 11.91 m

Hence the height of the building = 11.91 + 2 = 13.91 m.