Question

Convert the average temperatures for each collected data point given below from °C to K. Plot the average cell potentials E (y-axis) vs T (x-axis). The plot should be approximately linear. Add a trendline to find the best linear fit and write down the y-intercept and slope (b and m from the linear equation) for the trendline below.

Average Temperature in °C - Average Cell Potential (V)

15 - 0.465
18 - 0.467
21 - 0.468
24 - 4.69
27 - 0.471
30 - 0.472
33 - 0.474

Answer 1

Step-by-step explanation:

The equation of above line , y = 0.0005x+ 0.458

This can be compared with y = mx+c

Hence slope, m = 0.0005 and Y-intercept, c = 0.458

Or it can be plotted manually where straight line has to be drawn touching maximum number of data points. After drawing a straight linear line, we need to take any two points from the straight line and slope is calculated

Slope,

`m = (y_2-y_1)/(x_2-x_1)`

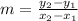
and y -intercept is calculated using extraplotting backwards such that it touches the Y-axis. the point where straight line touches Y-axis is Y-intercept (c).

Plot the average cell potentials E (y-axis) vs T (x-axis). image attached