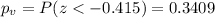Question

A manufacturer claims that fewer than 6% of its fax machines are defective. In a random sample of 97 such fax machines, 5% are defective. Find the P-value for a test of the manufacturer's claim. Group of answer choices 0.3264 0.1736 0.3409 0.1591

Answer 1

`z=\frac{0.05 -0.06}{\sqrt{(0.06(1-0.06))/(97)}}=-0.415`

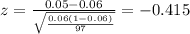
Now we can find the p value with the following probability:

`p_v =P(z<-0.415)=0.3409`

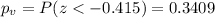
Explanation:

Information given

n=97 represent the random sample taken

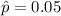`\hat p=0.05` estimated proportion of defective

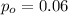`p_o=0.06` is the value to verify

z would represent the statistic

`p_v` represent the p value

Hypothesis to tests

We want to tet if the true proportion is less than 6%, the system of hypothesis are:

Null hypothesis:
`p\geq 0.06`

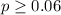
Alternative hypothesis:
`p < 0.06`

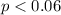
The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.05 -0.06}{\sqrt{(0.06(1-0.06))/(97)}}=-0.415`

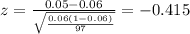
Now we can find the p value with the following probability:

`p_v =P(z<-0.415)=0.3409`