Answer:
The calculated value t = 1.76 < 2.131 at 0.05 level of significance
Null hypothesis is accepted
The manufacturer’s claim is greater than 560 bags per hour
Explanation:
Explanation:-
Given sample size 'n' =16
Given the manufacturer of an airport baggage scanning machine claims it can handle an average of 560 bags per hour.
mean of the Population 'μ' = 560
Mean of the sample Χ⁻ = 538
sample standard deviation' S' = 50
Null hypothesis:H₀:μ > 560
Alternative Hypothesis:H₁ : :μ < 560 (left tailed test)
Test statistic
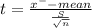
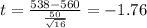
|t| = |-1.76| = 1.76
Degrees of freedom
γ = n-1 =16-1 =15
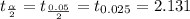
Conclusion:-
The calculated value t = 1.76 < 2.131 at 0.05 level of significance
Null hypothesis is accepted
The manufacturer’s claim is greater than 560 bags per hour