Question

A vertical spring-mass system undergoes damped oscillations due to air resistance. The spring constant is 2.65 ✕ 104 N/m and the mass at the end of the spring is 11.7 kg. (a) If the damping coefficient is b = 4.50 N · s/m, what is the frequency of the oscillator? Hz

Answer 1

f = 7.57 Hz

Step-by-step explanation:

To find the frequency of the damping oscillator, you first use the following formula for the angular frequency:

`\omega=\sqrt{\omega_o-((b)/(2m))^2}=\sqrt{(k)/(m)-((b)/(2m))^2}\\\\` (1)

k: spring constant = 2.65*10^4 N/m

m: mass = 11.7 kg

b: damping coefficient = 4.50 Ns/m

You replace the values of k, m and b in the equation (1):

`\omega=\sqrt{(2.65*10^4N/m)/(11.7kg)-((4.50Ns/m)/(2(11.7kg)))^2}\\\\\omega=47.59(rad)/(s)`

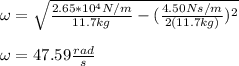
Finally, you calculate the frequency:

`f=(\omega)/(2\pi)=(47.59)/(2\pi)Hz=7.57\ Hz`

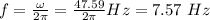
hence, the frequency of the oscillator is 7.57 Hz