Question

With a height of 68 ​in, Nelson was the shortest president of a particular club in the past century. The club presidents of the past century have a mean height of 70.7 in and a standard deviation of 2.3 in. a. What is the positive difference between Nelson​'s height and the​ mean? b. How many standard deviations is that​ [the difference found in part​ (a)]? c. Convert Nelson​'s height to a z score. d. If we consider​ "usual" heights to be those that convert to z scores between minus2 and​ 2, is Nelson​'s height usual or​ unusual?

Answer 1

a. The positive difference between Nelson's height and the population mean is:
`\\ \lvert 68-70.7 \rvert = \lvert 70.7-68 \rvert\;in = 2.7\;in`.

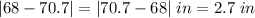b. The difference found in part (a) is 1.174 standard deviations from the mean (without taking into account if the height is above or below the mean).

c. Nelson's z-score:
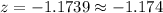`\\ z = -1.1739 \approx -1.174` (Nelson's height is below the population's mean 1.174 standard deviations units).

d. Nelson's height is usual since
`\\ -2 < -1.174 < 2`.

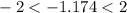Explanation:

The key concept to answer this question is the z-score. A z-score "tells us" the distance from the population's mean of a raw score in standard deviation units. A positive value for a z-score indicates that the raw score is above the population mean, whereas a negative value tells us that the raw score is below the population mean. The formula to obtain this z-score is as follows:

`\\ z = (x - \mu)/(\sigma)` [1]

Where

`\\ z` is the z-score.

`\\ \mu` is the population mean.

`\\ \sigma` is the population standard deviation.

From the question, we have that:

• Nelson's height is 68 in. In this case, the raw score is 68 in
  `\\ x = 68` in.
• 
  `\\ \mu = 70.7`in.
• 
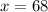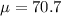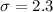  `\\ \sigma = 2.3`in.

With all this information, we are ready to answer the next questions:

a. What is the positive difference between Nelson​'s height and the​ mean?

The positive difference between Nelson's height and the population mean is (taking the absolute value for this difference):

`\\ \lvert 68-70.7 \rvert = \lvert 70.7-68 \rvert\;in = 2.7\;in`.

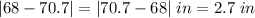That is, the positive difference is 2.7 in.

b. How many standard deviations is that​ [the difference found in part​ (a)]?

To find how many standard deviations is that, we need to divide that difference by the population standard deviation. That is:

`\\ (2.7\;in)/(2.3\;in) \approx 1.1739 \approx 1.174`

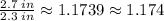
In words, the difference found in part (a) is 1.174 standard deviations from the mean. Notice that we are not taking into account here if the raw score, x, is below or above the mean.

c. Convert Nelson​'s height to a z score.

Using formula [1], we have

`\\ z = (x - \mu)/(\sigma)`

`\\ z = (68\;in - 70.7\;in)/(2.3\;in)`

`\\ z = (-2.7\;in)/(2.3\;in)`

`\\ z = -1.1739 \approx -1.174`

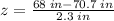
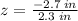
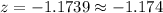
This z-score "tells us" that Nelson's height is 1.174 standard deviations below the population mean (notice the negative symbol in the above result), i.e., Nelson's height is below the mean for heights in the club presidents of the past century 1.174 standard deviations units.

d. If we consider​ "usual" heights to be those that convert to z scores between minus2 and​ 2, is Nelson​'s height usual or​ unusual?

Carefully looking at Nelson's height, we notice that it is between those z-scores, because:

`\\ -2 < z_(Nelson) < 2`

`\\ -2 < -1.174 < 2`

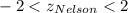
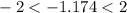
Then, Nelson's height is usual according to that statement.