Question

A. Suppose the laser light has wavelength 400 nm, and that the two small slits, which act as point sources of light, are separated by 0.1 mm. (Recall that 1 nm = 10-9 meters.) Approximately how many nodal lines would be present in the pattern of overlapping light waves when the laser light emerges from the two slits in the mask?

Answer 1

200 nodal lines

Step-by-step explanation:

To find the number of lines you first use the following formula for the condition of constructive interference:

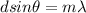`dsin\theta=m\lambda` (1)

d: distance between slits = 0.1mm = 0.1*10^-3 m

θ: angle between the axis of the slits and the m-th fringe of interference

λ: wavelength of light = 400 nm = 400*10^-9 m

You obtain the max number of lines when he angle is 90°. Then, you replace the angle by 90° and solve the equation (1) for m:

`dsin90\°=m\lambda\\\\d=m\lambda\\\\m=(d)/(\lambda)=(0.1*10^(-3)m)/(500*10^(-9)m)=200`

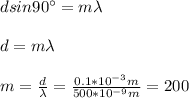
hence, the number of lines in the interference pattern are 200