Question

An Archer shoots an arrow horizontally at 250 feet per second. The bullseye on the target and the arrow are initially at the same height. If the target is 60 feet from the archer, how far below the bullseye (in feet) will the arrow hit the target

Answer 1

8.7

Explanation:

on edge . You're welcome

Answer 2

1.84feet

Explanation:

Using the formula for finding range in projectile, Since range is the distance covered in the horizontal direction;

Range
`R = U\sqrt{(H)/(g) }`

U is the velocity of the arrow

H is the maximum height reached = distance below the bullseye reached by the arrow.

R is the horizontal distance covered i.e the distance of the target from the archer.

g is the acceleration due to gravity.

Given R = 60ft, U = 250ft/s, g = 32ft/s H = ?

On substitution,

`60 = 250\sqrt{(H)/(32)} \\(60)/(250) = \sqrt{(H)/(32)}\\(6)/(25) = \sqrt{(H)/(32)`

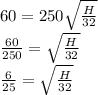
Squaring both sides we have;

`((6)/(25) )^(2) = (\sqrt{(H)/(32) } )^(2) \\(36)/(625) = (H)/(32) \\625H = 36*32\\H = (36*32)/(625) \\H = 1.84feet`

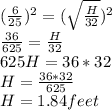
The arrow will hit the target 1.84feet below the bullseye.