Question

Two blocks can collide in a one-dimensional collision. The block on the left hass a mass of 0.30 kg and is initially moving to the right at 2.4 m/s toward a second block of mass 0.80 kg that is initially at rest. When the blocks collide, a cocked spring releases 1.2 J of energy into the system. (For velocities, use to mean to the right, - to mean to the left).A) What is the velocity of the first block after the collision?

B) What is the velocity of the second block after the collision?

Answer 1

a) 3.632 m/s

b) 0.462 m/s

Step-by-step explanation:

Using the law of conservation of momentum:

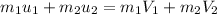`m_(1) u_(1) + m_(2) u_(2)= m_(1) V_(1) + m_(2) V_(2)`..........(1)

`m_(1) = 0.30 kg\\u_(1) = 2.4 m/s\\m_(2) = 0.80 kg\\u_(2) = 0 m/s`

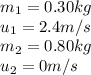
Substituting the above values into equation (1) and make V2 the subject of the formula:

`0.3(2.4) + 0.80(0)= 0.3 V_(1) + 0.8 V_(2)\\`

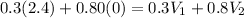
`V_(2) = (0.72 - 0.3 V_(1))/(0.8)`..................(2)

Using the law of conservation of kinetic energy:

`0.5m_(1) u_(1) ^(2) + 1.2 = 0.5m_(1) V_(1) ^(2) + 0.5m_(2) V_(2) ^(2)\\0.5(0.3) (2.4) ^(2) + 1.2 = 0.5(0.3) V_(1) ^(2) + 0.5(0.8)V_(2) ^(2)\\`

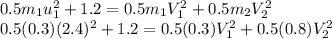
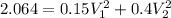`2.064 = 0.15 V_(1) ^(2) + 0.4V_(2) ^(2)`.......(3)

Substitute equation (2) into equation (3)

`2.064 = 0.15 V_(1) ^(2) + 0.4((0.72 - 0.3V_(1) )/(0.8)) ^(2)\\2.064 = 0.15 V_(1) ^(2) + 0.4((0.5184 - 0.432V_(1) + 0.09V_(1) ^(2) )/(0.64)) \\1.32096 = 0.096 V_(1) ^(2) + 0.20736 - 0.1728V_(1) + 0.036V_(1) ^(2) \\0.132 V_(1) ^(2) - 0.1728V_(1) - 1.1136 = 0\\V_(1) = 3.632 m/s`

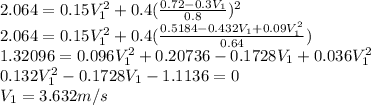
Substituting
`V_(1)` into equation(2)

`V_(2) = (0.72 - 0.3 *3.632)/(0.8)\\V_(2) = (0.72 - 0.3 *(3.632))/(0.8)\\V_(2) = 0.462 m/s`