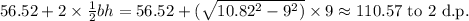Answer:
See below.
Explanation:
1) We know that the circumference of a circle can be found using the formula
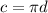 , so for this circle the circumference will be
, so for this circle the circumference will be
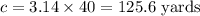 . The formula for the area of a circle is
. The formula for the area of a circle is
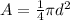 , so the area of this circle will be
, so the area of this circle will be
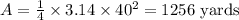 .
.
2) First we'll work out the length of the curved side of the shape. That's
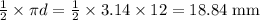 . Then, we'll add the length of the other two straight sides to get
. Then, we'll add the length of the other two straight sides to get
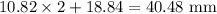 . Next: the area of the semi-circle is
. Next: the area of the semi-circle is
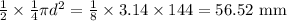 . Adding this to the areas of the two triangles:
. Adding this to the areas of the two triangles: