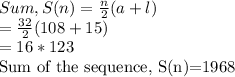Question

Find the sum of the sequence: 108, 105, 102,...,15

Answer 1

1968

Explanation:

The given sequence is a finite arithmetic sequence.

Step 1: Determine the number of terms in the sequence

For an arithmetic sequence, the nth term:

A(n)=a+(n-1)d

In the sequence:

• First term, a=108
• Last term, l=15
• Common difference, d=105-108= -3

Therefore, to find which term the number 15 is, we have:

15=108+(n-1)(-3)

15=108-3n+3

15=111-3n

3n=111-15

3n=96

Number of terms in the sequence, n=32

Step 2: Find the sum of the sequence

For an arithmetic sequence with a given first and last term:

`Sum, S(n)=(n)/(2)(a+l)\\ =(32)/(2)(108+15)\\=16*123\\$Sum of the sequence, S(n)=1968`