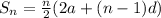Question

What is the sum of this arithmetic series?

Answer 1

The sum of the arithmetic series

`S_(n) = (n)/(2) (2 a + (n-1) d)`

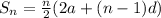
Explanation:

Explanation

Let a , a+d , a+2 d , ..........a+(n-1)d +....... is an arithmetic sequence

The sum of the sequence is called arithmetic series

The
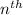`n^(th)` term of the sequence

`t_(n) = a + (n-1) d`

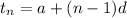
The sum of the arithmetic series

`S_(n) = (n)/(2) (2 a + (n-1) d)`

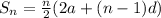
Here 'a' is the first term of the sequence

and 'd' be the difference between two values

sum of first term

put n=1 ⇒
`S_(1) = a`

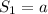
Put n =2 ⇒
`S_(2) = (2)/(2) (2 a + (2-1)d)`

`S_(2) = 2 a + d`

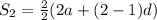
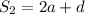
......and so on

The sum of the arithmetic series

`S_(n) = (n)/(2) (2 a + (n-1) d)`