Answer:
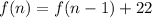 .
.
Explanation:
Note: In the given function it should be (n-1) instead of (n=1).
Consider the given function is
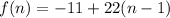
It is the explicit form of an A.P.
For
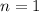 ,
,
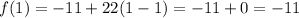
For
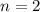 ,
,
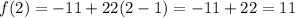
Common difference is

The recursive formula of an A.P. is
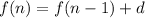
Substitute
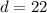 in the above formula.
in the above formula.
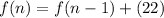
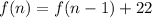
Therefore, required recursive formula is
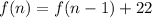 .
.