Answer:
Surface area of the pyramid = 157.99 in²
Explanation:
Volume of a pyramid is given by the formula,
Volume =
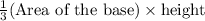
100 =
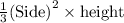
300 = s² × 5
s² = 60
s = √60
s = 2√15 in ≈ 7.746 in
Now surface area of the pyramid = Area of base + 4×(Area of one lateral side)
Area of square base = (Side)² = 60 in
Area of one lateral side =
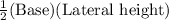
Since Lateral height =
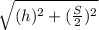 [By applying Pythagoras theorem in the given triangle]
[By applying Pythagoras theorem in the given triangle]
=

=
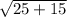
=
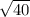
= 6.325 in.
Now area of lateral side =
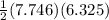
= 24.497 in²
Surface area of the pyramid = 60 + (4×24.497)
= 60 + 97.987
= 157.987 in²
≈ 157.99 in²