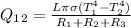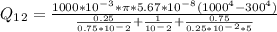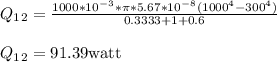Question

A heater rod (10 mm diameter, 100 mm length) of emissivity 0.75 is enclosed within a hollow cylindrical vacuum chamber (50 mm diameter, 100 mm length) of emissivity 0.25. The entire setup is insulated at the top and bottom ends by a low emissivity material, preventing any conductive heat dissipation from the ends. The heater rod is known to have a surface temperature of 1000 K, while the vacuum chamber is at a surface temperature of 300 K. How much heat is dissipated from the heater rod to the vacuum chamber (W)

Answer 1

Step-by-step explanation:

Given that:

Heater temperature ,T₁ = 1000K

Vaccum Chamber ,T₂ = 300K

emissivity of heater E₁ = 0.75

emissivity vaccum E₂ = 0.25

Heater diameter d₁ = 10 * 10⁻³mm

vaccum chamber d₂ = 50 * 10⁻³mm

When there is vaccum, then no air resistance will be there,

F₁₂ = 1

F₁₁ = 0

`R_1= (1-E_1)/(E_1A_1) \\\\=(1-0.75)/(0.75*\pi * 10^-^2*L)`

`R_2=(1)/(F_1_2 * A_1) \\\\=(1)/(1* \pi *10^-^2*L)`

`R_3=(1-0.25)/(F_1_2 * A_1) \\\\=(1)/(0.25* \pi *5*10^-^2*L)`

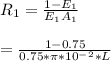
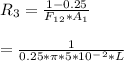
Heat leaving from heater surface 1 to vaccum

`Q_1_2 = (L \pi \sigma (T_1^4- T_2^4))/(R_1+R_2+R_3)`

`Q_1_2 = (1000*10^-^3*\pi * 5.67*10^-^8(1000^4-300^4))/((0.25)/(0.75*10^-2)+(1)/(10^-2) +(0.75)/(0.25*10^-^2*5) )`

`Q_1_2 = \frac{1000*10^-^3*\pi * 5.67*10^-^8(1000^4-300^4)} {0.3333+1+0.6}\\\\Q_1_2= 91.39 \text {watt}`