Question

In a random sample of 49 people who work out in the morning it is found that they exercise an average of 4.1 hours per weeks with a standard deviation of 0.7 hours. In a random sample of 54 people who exercise in the afternoon or evening it is found they exercise an average of 3.7 hours with a standard deviation of 0.5 hours. Test the claim that people who exercise in the morning have a mean exercise time greater than those who work out in the afternoon or evening at a 5% level of significance. a. Identify the parameter and label all given information. b. Identify the null hypothesis and the alternative hypothesis and identify the claim. c. Find the critical value(s). d. Compute the test statistic and/or find the p-value. e. State the conclusion that addresses the original claim. Upload

Answer 1

a)
`\mu_m -\mu_a`

`\bar X_(m)=4.1` represent the mean for the morning

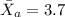`\bar X_(a)=3.7` represent the mean for the afternoon

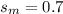`s_(m)=0.7` represent the sample standard deviation for the morning

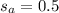`s_(a)=0.5` represent the sample standard deviation for afternoon

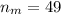`n_(m)=49` sample size for the morning

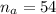`n_(a)=54` sample size for the afternoon

b) Null hypothesis:
`\mu_(m) \leq \mu_(a)`

Alternative hypothesis:
`\mu_(m) > \mu_(a)`

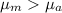
c)
`t_(\alpha)= 1.66`

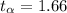
d)
`t=\frac{4.1-3.7}{\sqrt{(0.7^2)/(49)+(0.5^2)/(54)}}}=3.307`

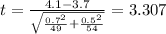
The p value would be:

`p_v =P(t_(101)>3.307)=0.00065`

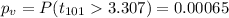
e) Since the calculated value is higher than the critical value we have enough evidence to reject the null hypothesis and we can conclude that the mean for people in the morning have a mean exercise time is greater than the mean for those who work out in the afternoon or evening at the 5% of significance

Explanation:

Part a

`\bar X_(m)=4.1` represent the mean for the morning

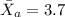`\bar X_(a)=3.7` represent the mean for the afternoon

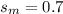`s_(m)=0.7` represent the sample standard deviation for the morning

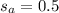`s_(a)=0.5` represent the sample standard deviation for afternoon

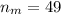`n_(m)=49` sample size for the morning

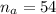`n_(a)=54` sample size for the afternoon

t would represent the statistic

`\alpha=0.05` significance level

The parameter of interest is:

`\mu_m -\mu_a`

Part b

We want to verify if the people who exercise in the morning have a mean exercise time greater than those who work out in the afternoon or evening, the system of hypothesis would be:

Null hypothesis:
`\mu_(m) \leq \mu_(a)`

Alternative hypothesis:
`\mu_(m) > \mu_(a)`

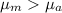
The statistic is given by:

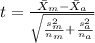`t=\frac{\bar X_(m)-\bar X_(a)}{\sqrt{(s^2_(m))/(n_(m))+(s^2_(a))/(n_(a))}}` (1)

Part c

Based on the significance level
`\alpha=0.05` and the degrees of freedom given by:

`df = 49+54-2= 101`

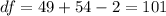
We can find the critical value in the t distribution iwth 101 degrees of freedom who accumuate 0.05 of the area in the right and we got:

`t_(\alpha)= 1.66`

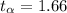
Part d

`t=\frac{4.1-3.7}{\sqrt{(0.7^2)/(49)+(0.5^2)/(54)}}}=3.307`

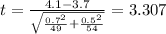
The p value would be:

`p_v =P(t_(101)>3.307)=0.00065`

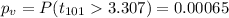
Part e

Since the calculated value is higher than the critical value we have enough evidence to reject the null hypothesis and we can conclude that the mean for people in the morning have a mean exercise time is greater than the mean for those who work out in the afternoon or evening at the 5% of significance