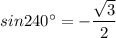Answer:
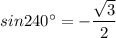
Explanation:
We are given that:
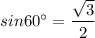
We need to find
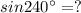
240 is greater than 180 and lesser than 270
OR
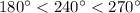
So, Angle
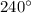 lies in the 3rd quadrant and it is well known that value of sine in 3rd quadrant is negative.
lies in the 3rd quadrant and it is well known that value of sine in 3rd quadrant is negative.
Using the property :
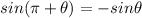 or
or
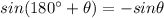
Here,
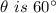 .
.
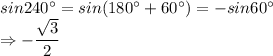
Hence, the value