Answer:
We want to test if the if p1 = the proportion of people who have myopia in 2019 is equal to p2 = proportion of people who have myopia in 2010 (alternative hypothesis) , then the system of hypothesis are:
Null hypothesis:
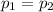
Alternative hypothesis:
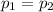
And the best option would be:
b. H0:P1=P2; Ha:P1≠P2
Explanation:
For this case we have the following info given:
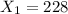 the myopia cases in 2019
the myopia cases in 2019
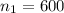 the sample size in 2019
the sample size in 2019
 estimated proportion of myopia cases in 2019
estimated proportion of myopia cases in 2019
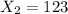 the myopia cases in 2010
the myopia cases in 2010
 the sample size in 2010
the sample size in 2010
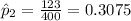 estimated proportion of myopia cases in 2010
estimated proportion of myopia cases in 2010
And we want to test if the if p1 = the proportion of people who have myopia in 2019 is equal to p2 = proportion of people who have myopia in 2010 (alternative hypothesis) , then the system of hypothesis are:
Null hypothesis:
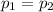
Alternative hypothesis:
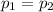
And the best option would be:
b. H0:P1=P2; Ha:P1≠P2
And we can conduct a two sample z proportion test in order to verify the hypothesis.