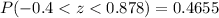Question

Use technology to solve the following problem: The mean annual income for people in a certain city (in thousands of dollars) is 44, with a standard deviation of 35. A pollster draws a sample of 59 people to interview. What is the probability that the sample mean income is between 42 and 48 (thousands of dollars)?

Answer 1

`P(42 < \bar X <48)`

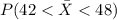
And we can use the z score formula given by:

`z =(\bar X -\mu)/((\sigma)/(√(n)))`

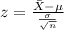
And if we find the z scores for the limits of the interval we got:

`z= (42-44)/((35)/(√(59)))= -0.4`

`z= (48-44)/((35)/(√(59)))= 0.878`

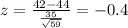
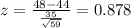
And we want to find this probability:

`P(-0.4<z<0.878)`

And we can use the foolowing excel command and we got:

=NORM.DIST(0.878;0;1;TRUE)-NORM.DIST(-0.4;0;1;TRUE)

And we got:

`P(-0.4<z<0.878)=0.4655`

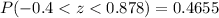
Explanation:

For this case we know the following parameters:

`\mu = 44 ,\sigma =35`

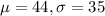
We select a sample size of n =59. So then the sample size is large enough to use the central limit theorem and the distribution for the sample mean is given by:

`\bar X \sim N(\mu (\sigma)/(√(n)))`

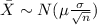
We want to find the following probability:

`P(42 < \bar X <48)`

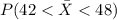
And we can use the z score formula given by:

`z =(\bar X -\mu)/((\sigma)/(√(n)))`

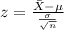
And if we find the z scores for the limits of the interval we got:

`z= (42-44)/((35)/(√(59)))= -0.4`

`z= (48-44)/((35)/(√(59)))= 0.878`

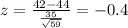
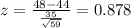
And we want to find this probability:

`P(-0.4<z<0.878)`

And we can use the foolowing excel command and we got:

=NORM.DIST(0.878;0;1;TRUE)-NORM.DIST(-0.4;0;1;TRUE)

And we got:

`P(-0.4<z<0.878)=0.4655`