Question

Line n is a perpendicular bisector of line segment T V. It intersects line segment T V at point R. Line n also contains points Q and S. Line segment R V is 3 x + 2. Line segment Q V is 4 x + 1. Line segment T S is 9 x minus 4. The length of TR is 17 units.

What are the lengths of SV and QT?

SV = units QT = units

Answer 1

SV = 41 units

QT = 21 units

Explanation:

Please refer to the attached figure.

It is given that line segment TV has a perpendicular bisector as line N which intersects on line on TV at point R.

So, TR = RV

We are given that:

`RV = 3 x + 2\\QV = 4 x + 1\\TS =9 x -4 \\TR = 17\ units`

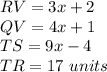
Comparing the values of TR and RV:

`3x +2=17\\\Rightarrow x = 5`

We can easily observe that due to the nature of the construction of this figure there is symmetry present.

As a result, we can draw the following conclusions:

1.
`QT = QV = 4x+1\\`

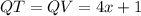
Putting value
`x=5`:

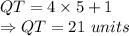
`QT = 4* 5+1\\\Rightarrow QT =21\ units`

2.
`TS =SV = 9x-4`

Putting value
`x=5`:

`\Rightarrow SV = 9 * 5-4\\\Rightarrow SV = 41\ units`

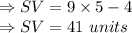
Hence the values are:

SV = 41 units

QT = 21 units