Question

The state education commission wants to estimate the fraction of tenth grade students that have reading skills at or below the eighth grade level. 1. Suppose a sample of 955 tenth graders is drawn. Of the students sampled, 812 read above the eighth grade level. Using the data, estimate the proportion of tenth graders reading at or below the eighth grade level. 2. Suppose a sample of 955 tenth graders is drawn. Of the students sampled, 812 read above the eighth grade level. Using the data, construct the 90% confidence interval for the population proportion of tenth graders reading at or below the eighth grade level.

Answer 1

The estimation for the proportion of tenth graders reading at or below the eighth grade level is given by:

`\hat p =(955-812)/(955)= 0.150`

`0.150 - 1.64 \sqrt{(0.150(1-0.150))/(955)}=0.131`

`0.150 + 1.64 \sqrt{(0.150(1-0.150))/(955)}=0.169`

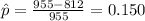
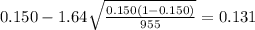
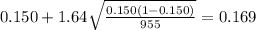
And the 90% confidence interval would be given (0.131;0.169).

Explanation:

We have the following info given:

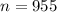`n= 955` represent the sampel size slected

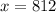`x = 812` number of students who read above the eighth grade level

The estimation for the proportion of tenth graders reading at or below the eighth grade level is given by:

`\hat p =(955-812)/(955)= 0.150`

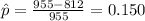
The confidence interval for the proportion would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

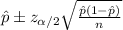
For the 90% confidence interval the significance is
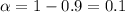`\alpha=1-0.9=0.1` and
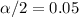`\alpha/2=0.05`, with that value we can find the quantile required for the interval in the normal standard distribution and we got.

`z_(\alpha/2)=1.64`

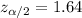
And replacing into the confidence interval formula we got:

`0.150 - 1.64 \sqrt{(0.150(1-0.150))/(955)}=0.131`

`0.150 + 1.64 \sqrt{(0.150(1-0.150))/(955)}=0.169`

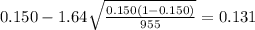
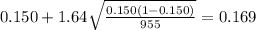
And the 90% confidence interval would be given (0.131;0.169).