Given Information:
Mean weekly salary = μ = $490
Standard deviation of weekly salary = σ = $45
Required Information:
P(X > $525) = ?
Answer:
P(X > $525) = 21.77%
Step-by-step explanation:
We want to find out the probability that a randomly selected teacher earns more than $525 a week.
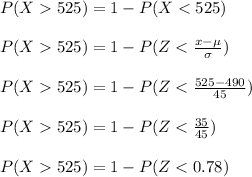
The z-score corresponding to 0.78 from the z-table is 0.7823
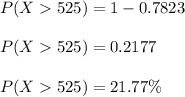
Therefore, there is 21.77% probability that a randomly selected teacher earns more than $525 a week.
How to use z-table?
Step 1:
In the z-table, find the two-digit number on the left side corresponding to your z-score. (e.g 0.7, 2.2, 1.5 etc.)
Step 2:
Then look up at the top of z-table to find the remaining decimal point in the range of 0.00 to 0.09. (e.g. if you are looking for 0.78 then go for 0.08 column)
Step 3:
Finally, find the corresponding probability from the z-table at the intersection of step 1 and step 2.