Answer:
The correct option is (B)
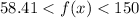 .
.
Explanation:
The exponential decay function is as follows:
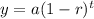
Here,
y = final value
a = initial value
r = decay rate
t = time taken
It is provided that:
a = 150 mg
r = 9% = 0.09
Then the next hour the amount of caffeine in the body will be:
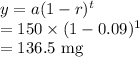
Then after two hours the amount of caffeine in the body will be:
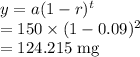
Similarly after 10 hours the amount of caffeine in the body will be:

Then the inequality representing the range of the exponential function that models this situation is:
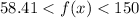
Thus, the correct option is (B).