Question

A recent study focused on the number of times men and women send a Twitter message in a day. The information is summarized below.

Men Sample size-25 Sample mean-20 Population standard deviation-5
Women Sample size-30 Sample mean-30 Population standard deviation-10
At the .01 significance level, is there a difference in the mean number of times men and women send a Twitter message in a day? What is the value of the test statistic for this hypothesis test?
1. 2.668
2. 2.672
3. 2.58
4. 2.40

Answer 1

The value of the test statistic = 2.58

Test statistic Z = - 4.805

|Z| = 4.805 > 2.58

Null hypothesis is rejected The value of the test statistic = 2.58

There is significant difference between in the mean number of times men and women send a Twitter message in a day

Explanation:

Step(i):-

Sample size of men n₁ = 25

mean of the first sample x₁⁻ = 20

Standard deviation of the first sample σ₁ = 5

Sample size of women n₂ = 30

mean of the second sample x₂⁻ = 30

Standard deviation of the first sample σ₂ = 10

Level of significance ∝= 0.01

Step(ii):-

Null Hypothesis : H₀: There is no significant difference between in the mean number of times men and women send a Twitter message in a day

Alternative Hypothesis :H₁:There is significant difference between in the mean number of times men and women send a Twitter message in a day

Test statistic

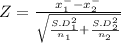
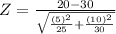
`Z = \frac{x^(-) _(1) - x^(-) _(2) }{\sqrt{(S.D_(1) ^(2) )/(n_(1) )+( S.D_(2) ^(2))/(n_(2) ) } }`

`Z = \frac{20 - 30 }{\sqrt{((5)^(2) )/(25 )+( (10)^(2) )/( 30) } }`

Z =
`(-10)/(2.081) = - 4.805`

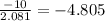
The value of the test statistic = 2.58 C

|Z| = 4.805 > 2.58

Null hypothesis is rejected The value of the test statistic = 2.58

Conclusion:-

There is significant difference between in the mean number of times men and women send a Twitter message in a day