Answer:
a) For this case and using the empirical rule we can find the limits in order to have 9% of the values:
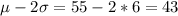
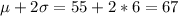
95% of the widget weights lie between 43 and 67
b) For this case we know that 37 is 3 deviations above the mean and 67 2 deviations above the mean since within 3 deviation we have 99.7% of the data then the % below 37 would be (100-99.7)/2 = 0.15% and the percentage above 67 two deviations above the mean would be (100-95)/2 =2.5% and then we can find the percentage between 37 and 67 like this:

c) We want to find the percentage above 49 and this value is 1 deviation below the mean so then this percentage would be (100-68)/2 = 16%
Explanation:
For this case our random variable of interest for the weights is bell shaped and we know the following parameters.

We can see the illustration of the curve in the figure attached. We need to remember that from the empirical rule we have 68% of the values within one deviation from the mean, 95% of the data within 2 deviations and 99.7% of the values within 3 deviations from the mean.
Part a
For this case and using the empirical rule we can find the limits in order to have 9% of the values:
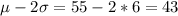
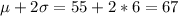
95% of the widget weights lie between 43 and 67
Part b
For this case we know that 37 is 3 deviations above the mean and 67 2 deviations above the mean since within 3 deviation we have 99.7% of the data then the % below 37 would be (100-99.7)/2 = 0.15% and the percentage above 67 two deviations above the mean would be (100-95)/2 =2.5% and then we can find the percentage between 37 and 67 like this:

Part c
We want to find the percentage above 49 and this value is 1 deviation below the mean so then this percentage would be (100-68)/2 = 16%